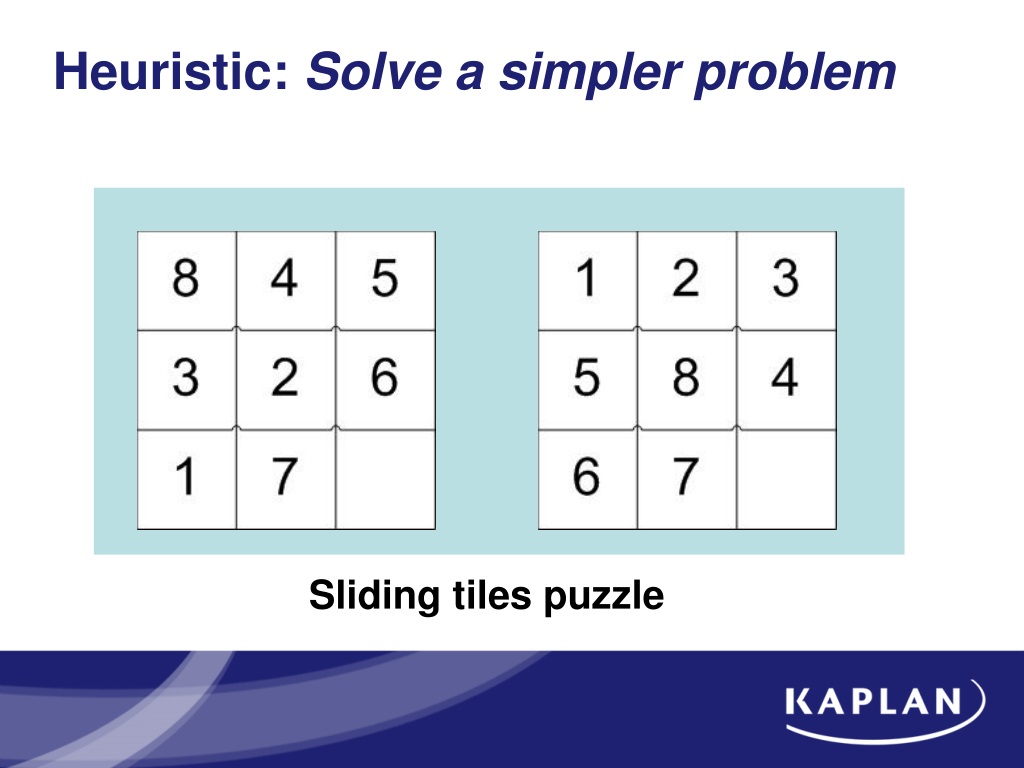
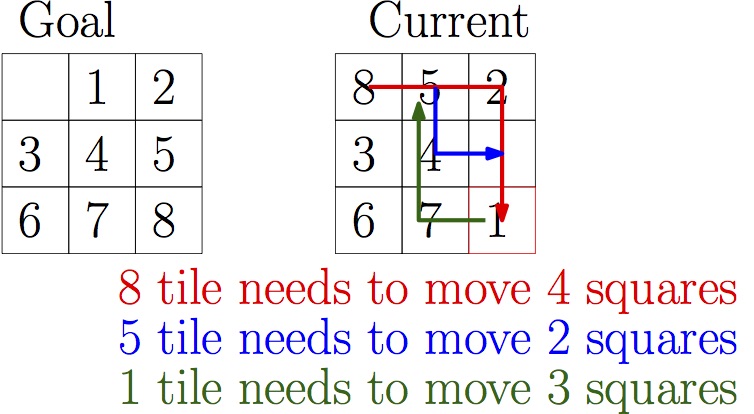
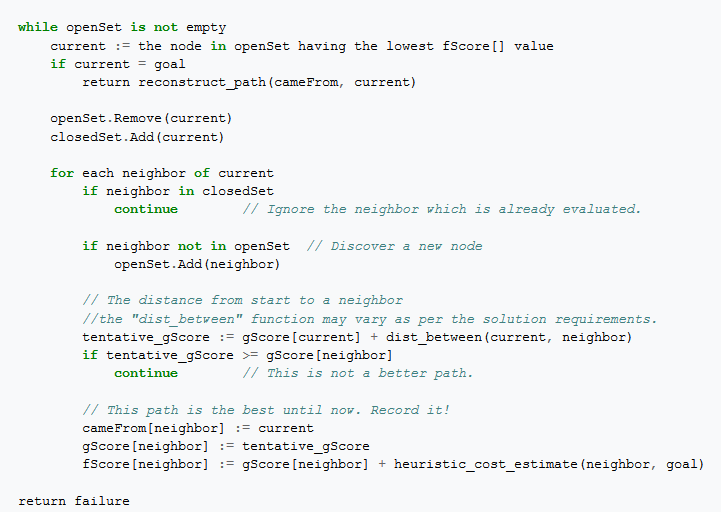
Hueristic To Solve A Siding Puzzle

To solve it by computer or ai we need a bit of a basic understanding of how it works to get the goal node.

Hueristic to solve a siding puzzle. Admissible heuristic let h n be the cost of the optimal path from n to a goal node the heuristic function h n is admissible 16 if. Breadth first search a or iterative deepening a ida. The number of nodes expanded and depth of solution. Essentially it means that even computers find it hard to come up with a solution source.

Sliding puzzles can be incredibly difficult to solve as anyone who s tried can tell you. 1 3 2 4 5 6 8 7 and goal state 1 2 3 8 4 7 6 5 i want to print out the running steps which solve this puzzle from initial to goal state this is the code i have so far. Implementation for a star and bfs algorithms to solve a nxn grid sliding puzzle problem. If you start with the top row and the left column you can solve slide puzzles of any size by breaking them into smaller and smaller grids.

Click on image for larger view figure 1. A 3 x 3 sliding tiles puzzles board. A employs a heuristic function to find the solution to a problem. The sliding tiles puzzle was created by chess player and puzzle maker sam loyd 1841 1911 in the 1870s.

The puzzle is divided into n 1 rows and n 1 columns eg. Gamestate class describes any game state in the search space. I am a student so i may be completely off base here. I am looking for code in java that implement a algorithm for the 8 puzzle game by given initial state.

15 puzzle will have 4 rows and 4 columns an 8 puzzle will have 3 rows and 3 columns and so on. Mathematicians categorize sliders as pspace complete which is a measure of their mathematical complexity. To compare the admissible heuristics mentioned earlier h1 to h4 one can generate a large number of initial states for the 8 puzzle and solve each one using all 4 heuristics. 0 h n h n an admissible heuristic function is always optimistic.

The current state as a list goal state as a list current level parent state and the used heuristic function and once it is initialized the heuristic score. By optimal solution we mean a solution requiring the minimum numbers of moves. The puzzle consists of a n x m board shown in figure 1 where each cell could be represented as a number a letter an image or basically anything you can think of. Solving 8 puzzle manually varies from person to person.

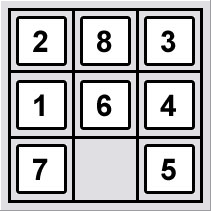
Keep solving the top row and leftmost column as many times as necessary until you have a 3x2 grid with five tiles left to arrange. A well designed heuristic would have a value of b close to 1. N puzzle or sliding puzzle is a popular puzzle that consists of n tiles where n can be 8 15 24 and so on. G is a goal node îh g 0 h n number of misplaced tiles 6 8 puzzle heuristics 4 1 7 5 2 3 6 8 state n 4 6 7 1 5 2 8 3 goal state.

It takes the following arguments. Good guide to the heuristic s overall usefullness. Sliding puzzle this application finds the optimal solution to solve a 8 or 15 puzzle.